Channel Coding and Modulation

Turbo Code and Concatenated Code
Prof Lajos Hanzo, Dr. Soon Xin Ng, Dr. Robert G. Maunder
[1] Iterative decoding convergence and termination of serially concatenated codes.
[2] Turbo Coding, Turbo Equalisation and Space-Time Coding: EXIT-Chart Aided Near-Capacity Designs for Wireless Channels.
[3] Turbo Decoding and Detection for Wireless Applications. [More Publications]

In his legendary contribution Shannon set out the performance limits of channel coding and modulation schemes as early as 1948. However, apart from Galleger’s radical idea of low density parity check (LDPC) codes disseminated as early as 1962, no schemes were capable of approaching Shannon’s capacity limits until the genesis of turbo codes in 1993. It remains a mystery, why the appealing concept of exploiting the so-called extrinsic information provided by the surrounding bits of a bit-stream for any bits in the stream remained largely unexploited before the invention of turbo codes. The now classic turbo-coding scheme is based on a composite codec constituted by two parallel concatenated codecs. Since their invention, turbo codes have evolved at an unprecedented pace and have reached a state of maturity within just a few years due to the intensive research efforts of the turbo coding community. As a result of this dramatic evolution, turbo coding has also found its way into standardized systems, such as, for example, the recently ratified third-generation (3G) mobile radio systems. Even more impressive performance gains can be attained with the aid of turbo coding in the context of video broadcast systems, where the associated system delay is less critical than in delaysensitive interactive systems.
[top]

Irregular Code and EXIT Chart Design
Prof Lajos Hanzo, Dr. Robert G. Maunder, Dr. Soon Xin Ng, Dr. Jing Wang
[1] Near-Capacity Irregular Variable Length Coding and Irregular Unity Rate Coding.
[2] Genetic Algorithm Aided Design of Component Codes for Irregular Variable Length Coding.
[3] Near-Capacity Variable-Length Coding: Regular and Exit-Chart Aided Irregular Designs. [More Publications]

Following the introduction of irregular LDPC codes, irregular coding was also applied in the context of turbo codes. These employ a parallel concatenation of two iteratively decoded CCs, which consider the original order of the source bits and an interleaved version, respectively. Whilst each source bit is encoded just once by each of the two parallel concatenated CCs in a regular turbo code, some source bits are encoded more than once by the CCs in the irregular scheme. As a result, it was possible to achieve a coding gain of 0.23 dB and operation within 25 dB of the channel’s Eb/N0 capacity bound by employing Monte Carlo simulations in order to find the required number of times that each source bit is encoded.

The serial concatenation and iterative decoding of an irregular outer code with a regular inner code was proposed by Tchler and Hagenauer. Here, the irregular outer code is comprised of N number of component codes, having a variety of inverted EXIT function shapes. These component codes are invoked for generating specific fractions of the encoded bit sequence, which may be specifically chosen in order to shape the irregular EXIT function.
Irregular Convolutional Codes (IrCC) were proposed by M. Tuchler and further characterised in [papers] . These typically employ a single mother CC to derive a suite of component CCs , which have a variety of coding rates that are obtained by using various generator polynomials in addition to the mother CC and/or by using puncturing.

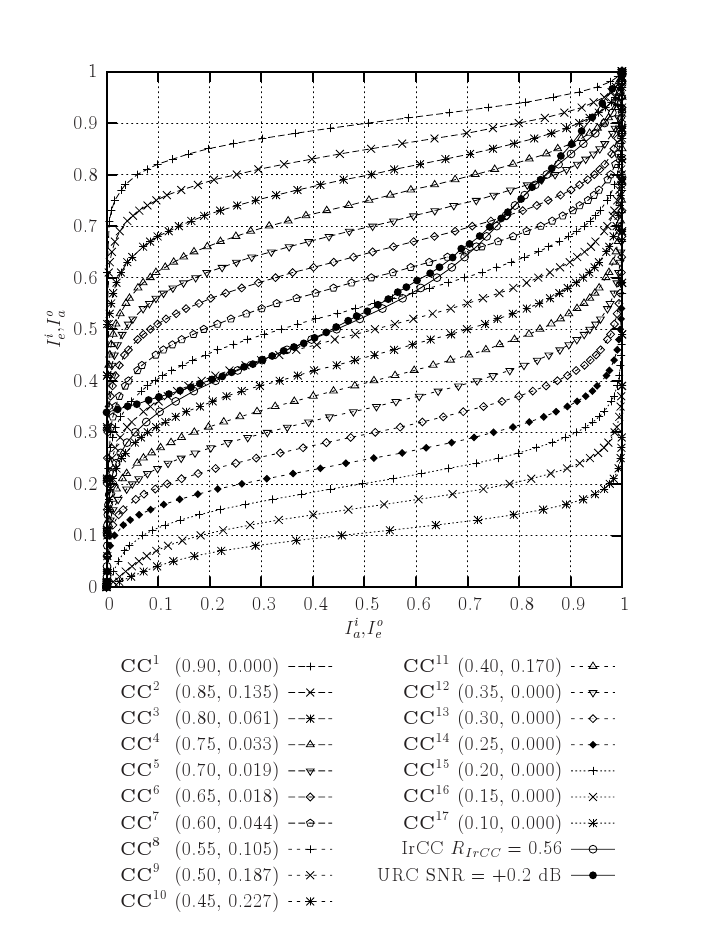
Figure 1: Inverted CC EXIT functions. The inverted EXIT function is provided for the corresponding IrCC arrangement, together with the URC EXIT function corresponding to a BPSK-modulated Rayleigh fading channel SNR of +0.2 dB. Inverted CC EXIT functions are labelled using the format CCn (R(CCn ), αn ).
Note that, the ability of EXIT chart matching to create narrow but still open EXIT chart tunnels depends on the availability of a suite of component codes having a wide variety of EXIT function shapes. However, in general it is challenging to design component codes having arbitrary EXIT function shapes, motivating the irregular code design process depicted in Figure 2. This advocates the design of diverse candidate component codes, the characterisation of their EXIT functions and the selection of a specific suite having a wide variety of EXIT function shapes, potentially involving a significant amount of ‘trial-and-error’ based human interaction. Following this, EXIT chart matching may be achieved by selecting the component fractions, as described above.

Figure 2: Conventional irregular coding design process.

The application of EXIT chart matching invoking Irregular Variable Length Coding(IrVLC) is motivated for the sake of near-capacity joint source and channel coding of source symbol sequences having values exhibiting unequal occurrence probabilities. Instead of the component CCs employed in IrCC schemes, the proposed IrVLC scheme employs component VLC codebooks. These have different coding rates and are used for encoding appropriatedly selected fractions of the input source sysmbol stream. In this way, the resultant composite inverted EXIT function may be shaped for ensuring that it does not cross the EXIT function of the inner channel codec.
[top]

LDPC Code, Rateless Code and Fountain Code
Prof Lajos Hanzo, Dr. Feng Guo, Dr. Nicholas Bonello, Dr. T. D. Nguyen, Mr. Xin Zuo
[1] Low-Density Parity-Check Codes and their Rateless Relatives.
[2] H-ARQ-Aided Systematic Luby Transform Codes.
[3] Reconfigurable rateless codes. [More Publications]

Looking back over the last five decades or so, one can reasonably surmise that the family of low-density parity-check codes (LDPC) and that of turbo codes, constitute the two most practical realizations of Shannon’s theory, which have revolutionized the field of error correction coding. It was precisely the year 1948, when Claude E. Shannon, who at that time was a researcher at Bell Labs, published one of the most important theories, which inspired the research community for many years to come. At that time, his theories disproved the widely supported belief that increasing the amount of information-carrying bits transmitted over the channel per second, imposes an increase in the probability of error. Shannon demonstrated that it is possible to transmit information arbitrarily reliably over any unreliable channel, provided that the information transmission rate is lower than the capacity of the channel. Therefore, the channel capacity sets the bound on how much information we can transmit over a channel.

Shannon’s claim can be realized by a technique referred to as forward error correction (FEC). The basic idea is that of incorporating redundant bits, or check bits, together with the original information bits, thus creating what is known as a codeword. If the check bits are introduced in a “appropriate manner” so as to make each codeword sufficiently distinct from each other, the receiver will then become capable of determining the most likely codeword that has been transmitted. The channel capacity will determine the exact amount of redundancy that has to be incorporated by the encoder in order to be able to correct the errors imposed by the channel. However, Shannon’s theory only quantifies the maximum attainable rate, but refrains from specifying the means of achieving it. This triggered widespread research efforts resulting in diverse extensions, deeper interpretations and practical realizations of Shannon’s original work, which reached its pinnacle in the definition of LDPC and turbo codes.
[top]

Coded Modulation, Superposition Coded Modulation and Sphere Packing Modulation
Prof Lajos Hanzo, Dr. Soon Xin Ng, Dr. Rong Zhang, Dr. Osamah Alamri
[1] Near-capacity turbo trellis coded modulation design based on EXIT charts and union bounds.
[2] Superposition-Coding Aided Multiplexed Hybrid ARQ Scheme for Improved End-to-End Transmission Efficiency.  
[3] Nonbinary LDPC-Coded Sphere-Packed Transmit Diversity. [More Publications]

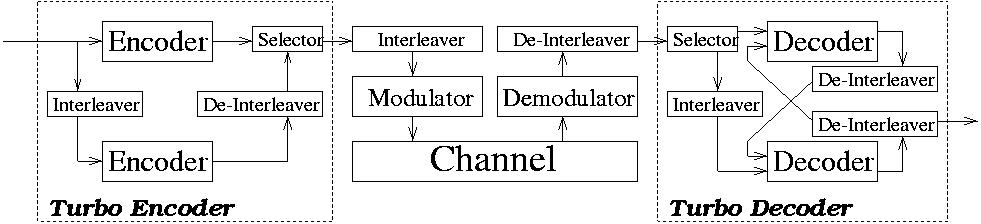
Figure 1 :Turbo Trellis-Coded Modulation scheme

In classical digital communication systems, modulation and error-correction coding are considered as two different entities. However, the combination of error-correction coding with modulation leads to the concept of Trellis-Coded Modulation (TCM). TCM is a bandwidth efficient scheme, where the redundancy introduced by the coding does not expand the bandwidth since the parity bits are absorbed by the extended signal constellation. One of the objecties of our research is to design TCM schemes for dispersive fading channels. As a further advance in channel coding, turbo coding was proposed in 1993. The databits are encoded twice and two decoders assist each other during decoding. This approach produces remarkable performance results, which are close to the Shannon limits. Turbo coding can be combined with trellis-coded modulation in order to produce Turbo TCM (TTCM) codes. The optimum design of TTCM scheme for dispersive fading channel is our goal in this field.
[top]

Hierarchical Modulation (HM), which is also known as layered modulation, has been widely adopted in industry nowadays. Its strict backward compatibility and low complexity let it becomes an efficient solution to the problems of upgrading wireless communication services. The potential employment of HM scheme in cooperative communications to increase the throughput and to lower the power consumption has drawn more and more attentions. Nowadays, the researchers had discussed several possible ways to combine HM scheme and CM scheme in cooperative communication system. The common choice is to use multiple lower modulation level encoder blocks and combine the independently coded bits by HM scheme to produce higher modulation level symbols.
In [1, 2], we have proposed a newly designed HM scheme aided cooperative communica- tion system and tried to optimized the performance of the entire system. Our assumption is that the Destination Node (DN) is only capable of receiving 4QAM signals from the Source Node (SN) due to the hostile nature of the fading channel. By contrast, our simulation results demonstrated that with the aid of our TTCHM scheme relying on a single relay, it is possible for the SN to transmit 16QAM or even 64QAM symbols, while maintaining an acceptable BER performance at the DN.

[top]